Machine Learning models don't just classify, they also approximate probabilities. Notice that the most important word in the previous sentence is written in bold. Approximations of probabilities can be very useful but one needs to be very careful. They should not directly be interpreted as an actual degree of certainty.

The goal of this document is convince you of this and to hint on how to solve this issue.

Example Dataset

To demonstrate this effect I will train a KNeighborsClassifier on a toy dataset that is generated by the scikit-learn api. The code for this is listed below as well as an image of the distribution of classes.

X, y = make_blobs(n_samples=1000, center_box=(-2, 2), random_state=42)

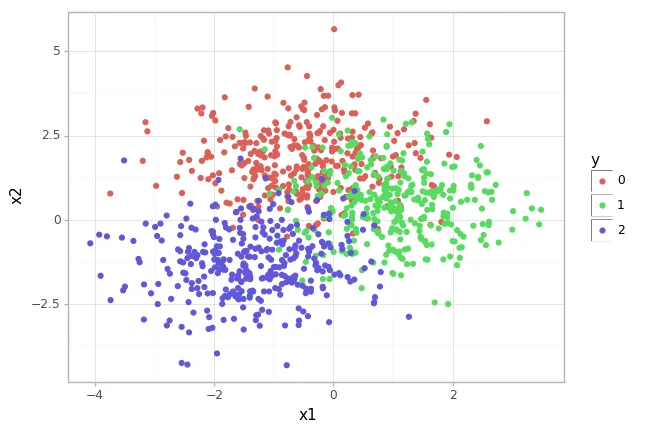
This is a dataset that is relatively easy to train and fit.

mod = KNeighborsClassifier(20, weights="distance").fit(X, y)

I've plotted the output of this model below. Areas where the algorithm has a probability value larger than 0.9 are highlighted.

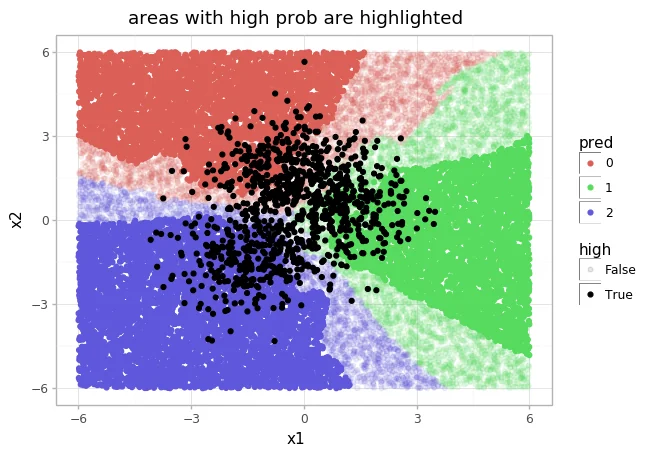
Notice that there is a lot of areas where the algorithm gives a very high probability but where the algorithm has never seen any data. This is, at least to me, feels very awkward. The algorithm suggests to give certainty to regions where it hasn't seen any data.

To emphesize this crazyness, let's zoom out a bit.

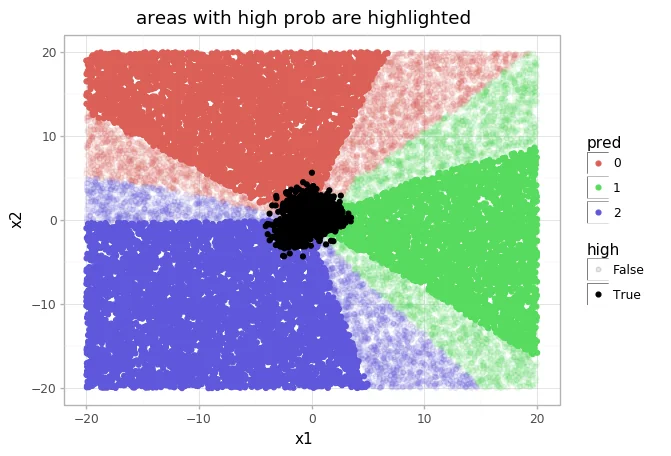
The area where the data actually resides in is smaller than the area where the algorithm suggests to be able to predict with certainty.

General Issue

One might think that this issue is caused by of our choice in algorithm. This is not true. To demonstrate this, consider the following results from other algorithms.

imgs <- c("output_8_0.png", 
          "output_9_0.png")
knitr::include_graphics(imgs)

This issue, it seems, is general.

General Problem

We should remember that the output from .predict_proba() is an approximation of a probability. It might be a proxy for probability but this is different from being a direct link to certainty. This is because machine learning models are often designed for interpolation, not extrapolation.

It would be less of an issue if machine learning models weren't designed to always give a result. There is usually no mechanism that assigns doubt to an outcome if a decision is made outside of a comfort zone.

Lucky for us, this last part of the problem can be fixed with a little bit of probability glue.

The Density Trick

What if we used an outlier detection algorithm to detect if a point we're trying to predict is outside of our comfort zone? One way of getting there is to use a Gaussian Mixture Model on our original dataset \(X\). We can measure what areas have likely values in \(X\) and with that we can say what area's aren't. This can be easily implemented thanks for scikit learn.

X, y = make_blobs(n_samples=1000, center_box=(-2, 2), random_state=42)
mod = KNeighborsClassifier(20, weights="distance").fit(X, y)
out = GaussianMixture(3).fit(X)

boundary = np.quantile(out.score_samples(X), 0.01)
simdf = (pd.DataFrame({"x1": np.random.uniform(-6, 6, n), 
                       "x2": np.random.uniform(-6, 6, n)})
         .assign(pred = lambda d: mod.predict(d.values).astype(np.object))
         .assign(prob = lambda d: out.score_samples(d[['x1', 'x2']].values) > boundary))

When we get new values then this learned boundary, or threshold, can be used to detect the region where we might be comfortable with interpolation. This result looks promising.

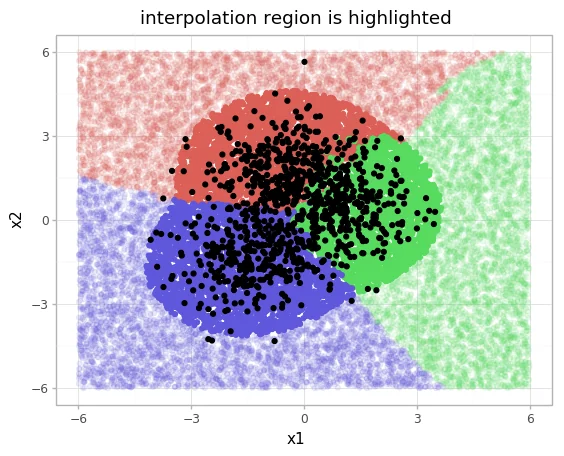
We seem to skip a few outliers but we can now design the system to only make a prediction when the point to predict is within the comfort zone. If it is outside of it, it can simply "not make a prediction".

Conclusion

Personally, I'm charmed by the idea of designing a predictive system that can say "Nope! Not predicting this one!". It sounds like a very sane way of dealing with uncertainty. Using an outlier algorithm as a cog in this system makes sense too. I personally like the idea of using a GMM for this because having a probability distribution as an output gives nice flexibility.

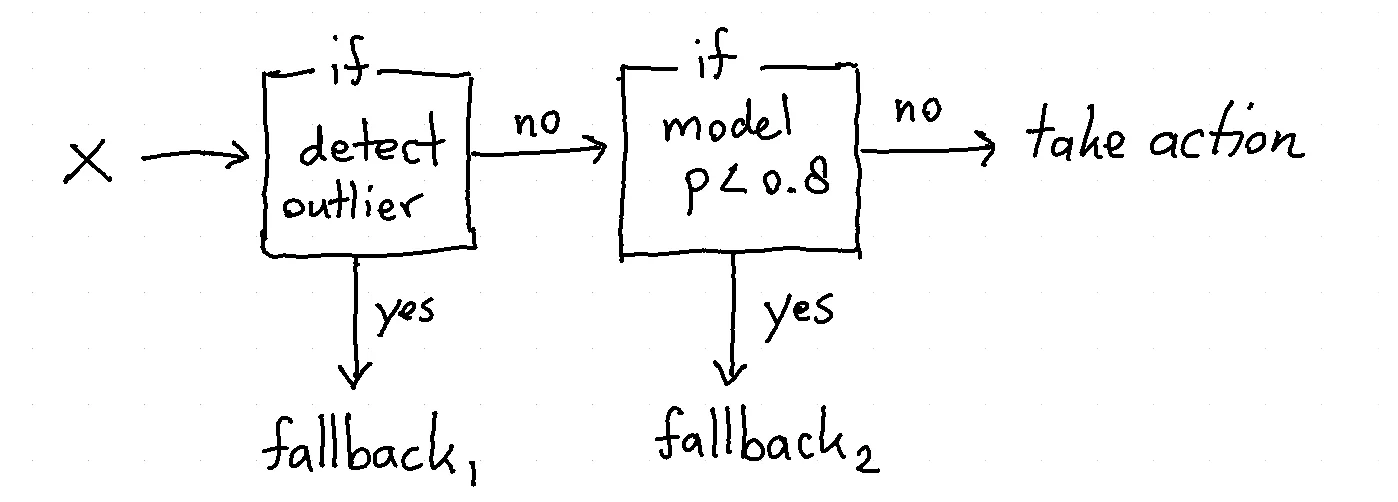
I wouldn't want to suggest that this idea is a free lunch though. Getting a GMM to fit your dataset well is still tricky business. Setting the right threshold isn't much fun either.

Sources

I've implemented this GMM outlier detection algorithm in scikit-lego. Feel free to use it.

If you want to play with the code used in this notebook, you can do so here.