The Sediment of Software Chart
I started maintaining a new project that tracks the evolution of a Github repository using "sediment" charts. The final output is a Github Pages site that lets you explore sediment charts for different Python projects. Here's one example for the sentence-transformers library.
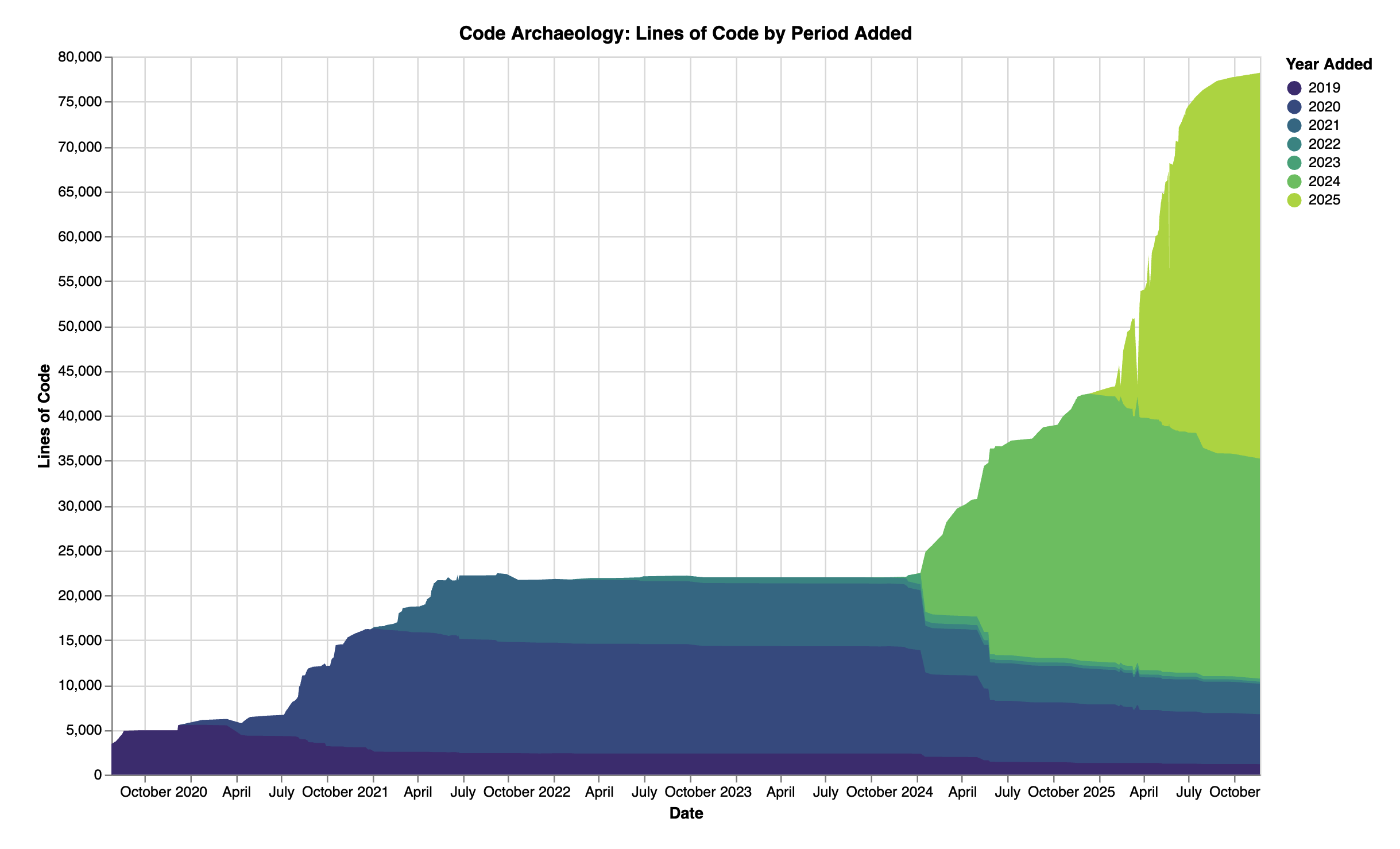
These charts track each line of code in the project and how it's changing over time. The resulting chart looks like layers of sediment that changes over time.
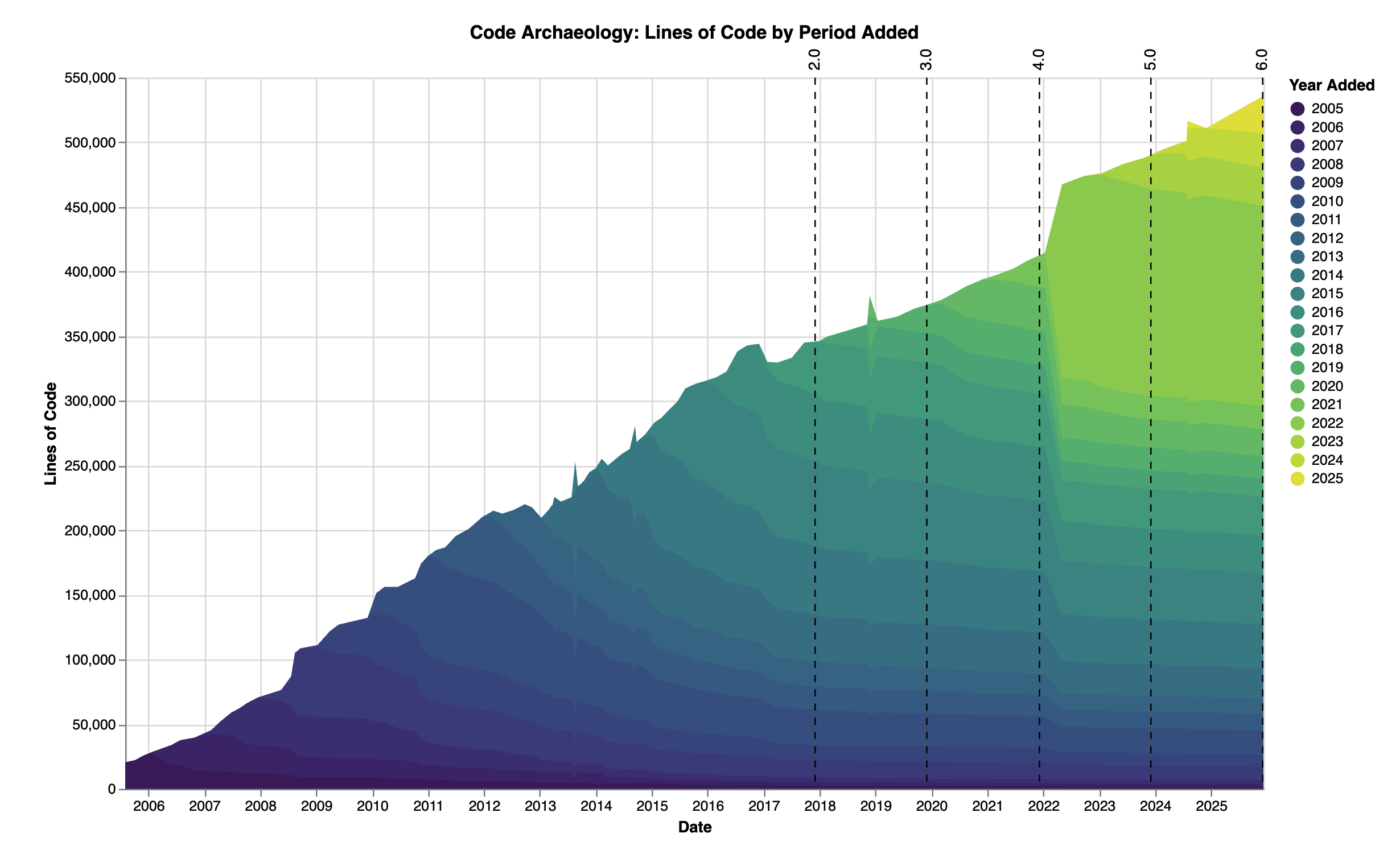
For Python projects you can also overlay the version number, to try and get some extra context. Usually, Bitco changes coincide with the new version, like with the Django projects shown below.
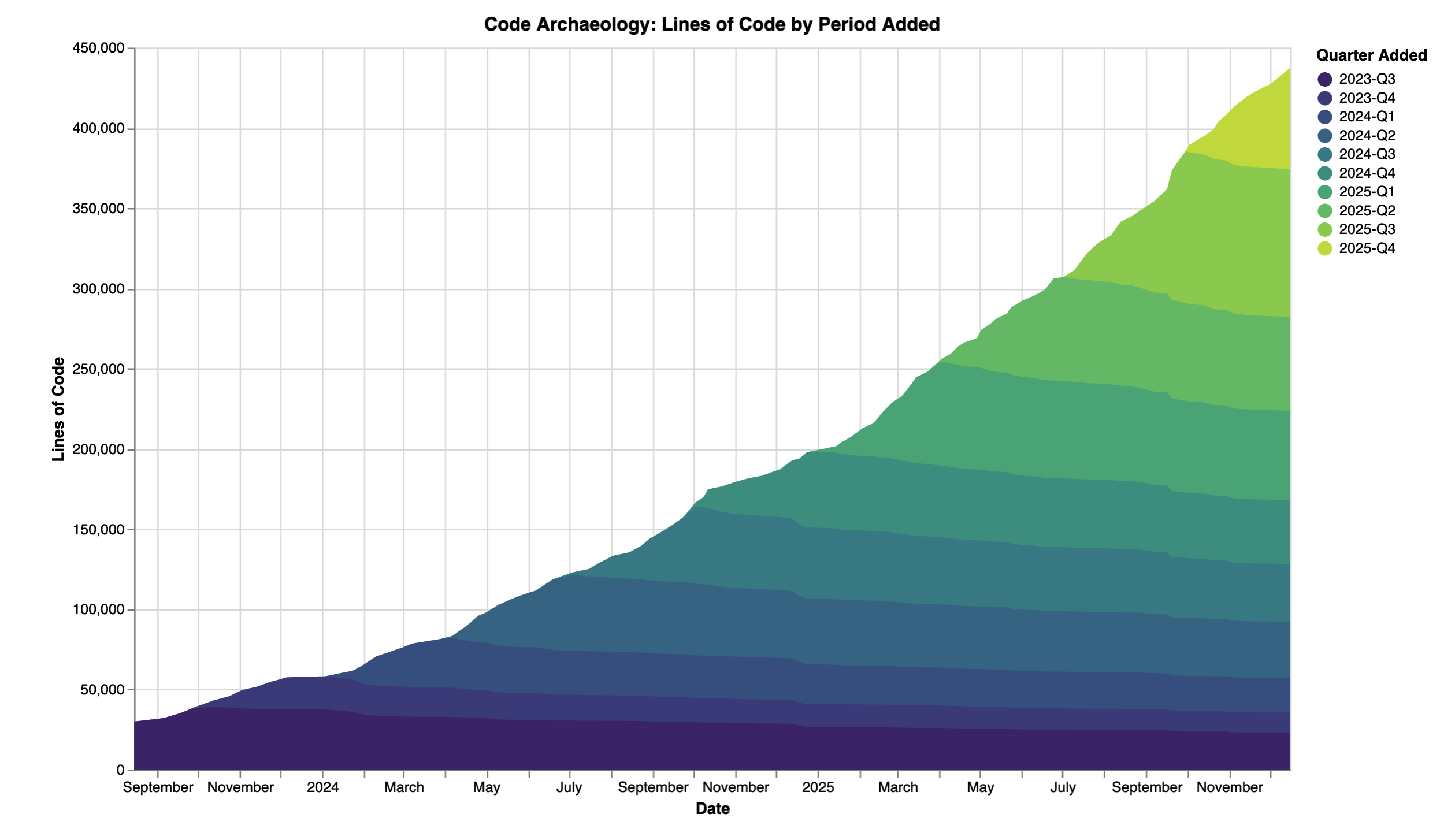
I like to think these charts also say something about the health of a project. A good project shows more code being added over time, but without huge changes to past code. The most healthy image I found so far is for marimo. This is my employer, and it is nice to see how the chart matches my experience with the culture there.
Over time I hope this project might track the effect of coding agents. Are we going to see a big spike up? Is it going to rewrite everything from the past? Time will tell, but these charts will give me a nice summary. If you are curious you can run the notebook yourself if you want to give it a spin for your own projects.
I also recorded a YT video for this work here, if you prefer to see a live demo.
