Theoretical Dependence

The simplest regression might look something like this;

\[ \hat{y}_i \approx \text{intercept} + \text{slope } x_i\]

You might assume at this point in time that the slope and intercept are unrelated to eachother. In econometrics you're even taught that this assumption is necessary. If you're one I have to warn you for what you're about to read. I'm about to show you why, by and large, this independance assumption is just plain weird.

Posterior

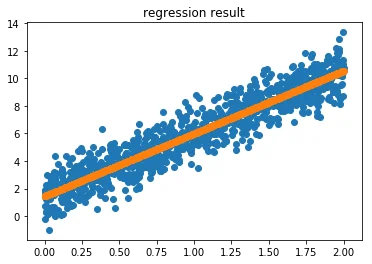
Let's generate some fake data and let's toss it in PyMC3.

import numpy as np
import matplotlib.pylab as plt

n = 1000
xs = np.random.uniform(0, 2, (n, ))
ys = 1.5 + 4.5 * xs + np.random.normal(0, 1, (n,))

PyMC3

Let's now throw this data into pymc3.

import pymc3 as pm

with pm.Model() as model:
    intercept = pm.Normal("intercept", 0, 1)
    slope = pm.Normal("slope", 0, 1)
    values = pm.Normal("y", intercept + slope * xs, 1, observed=ys)
    trace = pm.sample(2000, chains=1)

plt.scatter(trace.get_values('intercept'), trace.get_values('slope'), alpha=0.2)
plt.title("pymc3 results");

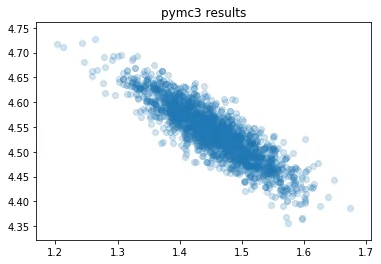
That's interesting; the intercept and slope variables aren't independant at all. They are negatively related!

Scikit-Learn

Don't trust this result? Let's sample subsets and throw it into scikit learn, let's see what comes out of that.

size_subset = 500
n_samples = 2000
samples = np.zeros((n_samples, 2))

for i in range(n_samples):
    idx = np.random.choice(np.arange(n), size=size_subset, replace=False)
    X = xs[idx].reshape(n_samples, 1)
    Y = ys[idx]
    sk_model = LinearRegression().fit(X, Y)
    samples[i, 0] = sk_model.intercept_
    samples[i, 1] = sk_model.coef_[0]

plt.scatter(samples[:, 0], samples[:, 1], alpha=0.2)
plt.title("sklearn subsets result");

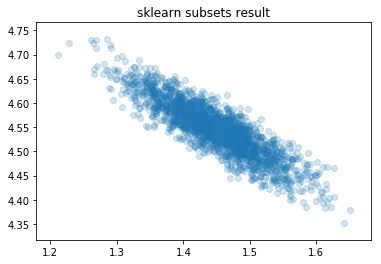
Why?

So what is going on here? We generated the data with two independent parameters. Why are these posteriors suggesting that there is a relationship between the intercept and slope?

There are two arguments to make this intuitive.

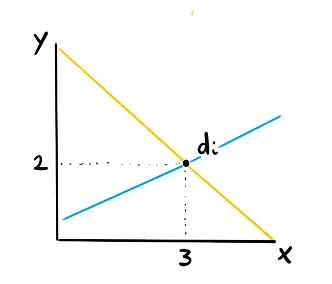
Argument One: Geometry

Consider these two regression lines that go into a single point.As far as the little point is concerned both lines are equal. They both have the same fit. We're able to exchange a little bit of the intercept with a little bit of the slope. Granted, this is for a single point, but also for a collection of points you can make an argument that you can exchange the intercept for the slope. This is why there must be a negative correlation.

When the intercept is low, the slope must be high to fit a single point.

Argument Two: A bit Causal

Consider this causal graph.

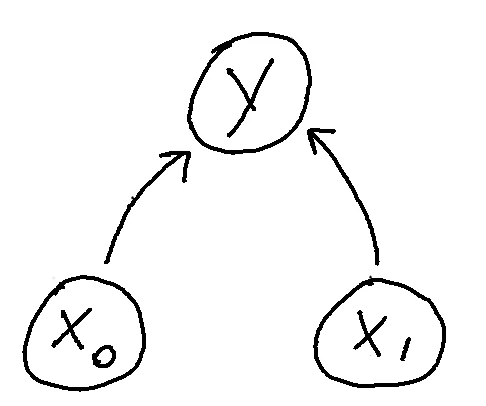
Given x_0, does our belief in x_1 update?

The $x_0$ node and $x_1$ node are independant, that is, unless $y$ is given. That is because, once $y_i$ is known, we're back to a single point and then the geometry argument kicks in. But also because logically we could explain the point $y_i$ in many ways; a lack of $x_0$ can be explained by an increase of $x_1$, vise versa or something in between. This encoded exactly in the graphical structure.

Conclusion

It actually took me a long time to come to grips with this. Upfront the linear regression does look like the addition of independant features. But since they all need to sum up to a number, it is only logical that they are related.

Assuming properties of your model upfront is best done via a prior, not by an independence assumption.

Appendix

The interesting thing about this phenomenon is that it is so pronounced in the simplest example. It is far less pronounced in large regressions with many features, like;

$$ y_i \approx \text{intercept} + \beta_1 x_{1i} + ... + \beta_f x_{fi} $$ Here's some plots of the intercept value vs. the first estimated feature, $\beta_1$ given $f$ features;

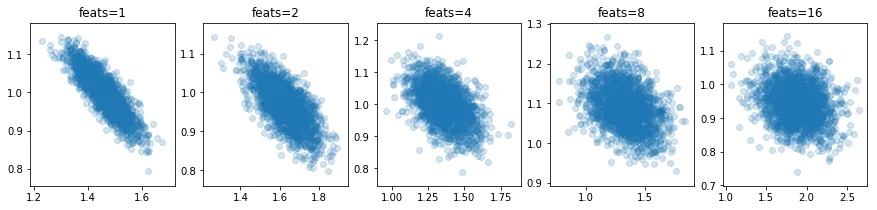
You can clearly see the covariance decrease as $f$ increases. The code for this can be found here.